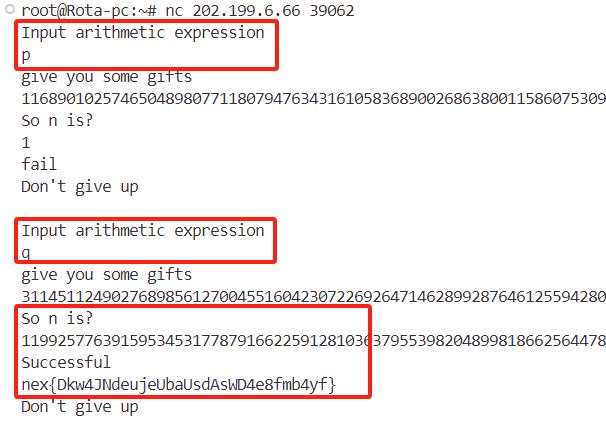
guess_number1

这题其实根本不用什么数论就能解，你只需知道模运算就好了。
另外可能看起来很难，实际上你如果仔细看下来，你会发现是很简单的，当你不知道为什么的时候，拿笔算算或者本地生成数据看看。

解法一

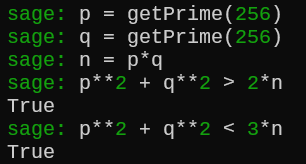
假设现在的情况是

p > q

那么有

p^{2} < n

及

q^{2} > n

当分别输入

p

和

q

时得到的实际上是

p^{2} (1)

q^{2} - n (2)

对于上面这两个数而言，只要把

p^{2}

和

q^{2}

消掉就能得到 n , 那

p^{2}

和

q^{2}

怎么来呢？
我们发现在模

n

下存在这样的性质，即输入

p + q

后真正得到的:

(p + q)^{2} = p^{2} + 2 * p * q + q^{2} = p^{2} + q^{2} (m o d n)

将其转换到实数域上得到：

p^{2} + q^{2} - 2 * n (3)

同样对于 $(p - q)^{2}$ 结果是一样的

那这为什么是 $2 * n$ 呢，最简单的方法就是拿数据测

现在答案已经很明显了，将 $(1)$ 和 $(2)$ 相加再减去 $(3)$ 即可得到 $n$ 。
再给大家推一下:

(p^{2}) + (q^{2} - n) - (p^{2} + q^{2} - 2 * n) = p^{2} + q^{2} - n - p^{2} - q^{2} + 2 * n = n

这种方法其实跟 $p, q$ 大小无关，反正把 $p, q$ 输进去的加起来, 然后减去输入 $p + q$ 的值就是 $n$

输入 $p, q$ ，然后将结果相加,再减去输入 $p + q$ 得到的结果就是 $n$

交互： alt text

解法二相比一来说需要开方和解方程，我更推荐解法一。
对于 $(1)$ 而言由于可以直接开方得到p，我使用的是gmpy2的isqrt函数:

from gmpy2 import *
p_2 = 
p = isqrt(p_2)
assert p**2 = p_2

isqrt有个缺陷就是它不会管你是不是完全平方数，如果不是会直接开出离数据最近的数

由于求出 $p$ 了然后对于 $(2)$ 而言，假设输入 $q$ 后返回的是c有:

q^{2} - p * q = c

大家其实可以发现这就是个一元二次方程，直接解方程就完事了，当然如果你用的是传统的解方程方法也是行的，我用的是sagemth：

var('q')
solve([q^2 - p*q == c],q)

然后解出来 $p$ 和 $q$ 后,

n = p * q

对 $p$ 或 $q$ 开个方，然后解个小学生可能会的一元二次方程，再把两数乘起来

交互:
alt text